| RETURN TO PROTEUS home |
| RETURN TO RISK HOMEPAGE |
| AVAILABLE: |
| SPECIAL TREES <<<< you are HERE |
TREES: EXAMPLES
Some examples of more advanced trees for calculating event-probabilities. In the first one we are examining the common question of reliability of tests (e.g. for diseases).
"If you have just been given the results of a test for a disease, what it the chance you actually have it?" The solution lies with the work on "prior probabilities" carried out by Thomas Bayes. The table always takes the form of a 2x2 tree with the population incidence on the left and the test results for the individual on the right.
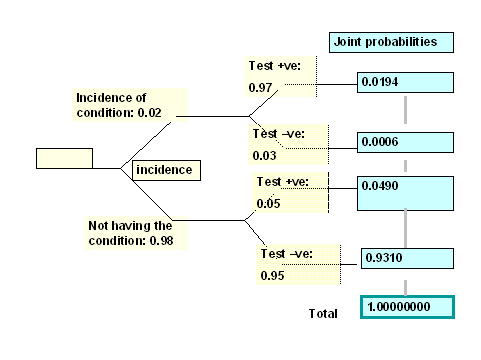
The question can be written P(D+|T+) and the solution is to take all T+ values (1st and 3rd joint probabilities) as your denominator, with the value you need (1st joint prob.) as the numerator.
so P(D+|T+) = ___ P(D+and T+)______ = _____0.0194_____ = 0.28363
P(D+and T+) + P(D-and T+) 0.0194 + 0.0490
This is the same as the formal formulaic expression:
P(D+|T+) = P(T+ and D+) Remember that P(T) is "all T+" thus P(D+and T+) + P(D-and T+)
P(T+)
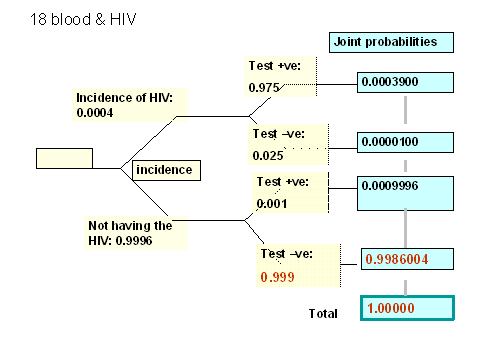
QUESTION 18 (Blood safety and HIV).....
This question is straightforward except for the tree which is easily constructed with an error. Note the information in the question which informs us that 1 in 100,000 transfusions are "test negative but virus positive." THIS IS NOT A CONDITIONAL PROBABILITY. It is a joint probability (P(V+ and T+) and so belongs in the second joint probability from the top in the chart below. The remainder of the tree is computed from this and the subsequent information.
QUESTION 20 AERO-ENGINES
ONE ENGINE, three hours flight with risk of failure 1/8000 per hour. The answer in this case is Very close to 3/8000, but technically it is not correct. P(NOTfail) is 7999/8000 or 0.999875 Raise this to third power (0.99962504). Compliment = 0.00037495 (Ans A)