Back to problems & solutions page
Back to ENH825 Main (LOG) page
SOLUTION: # 19 in course handbook

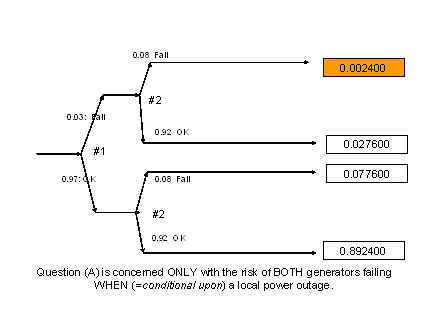
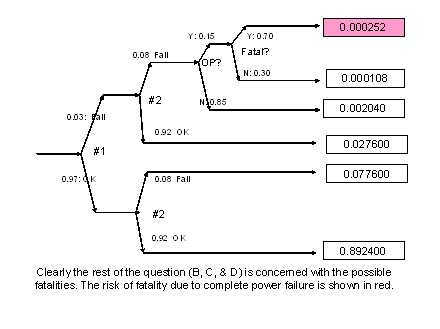
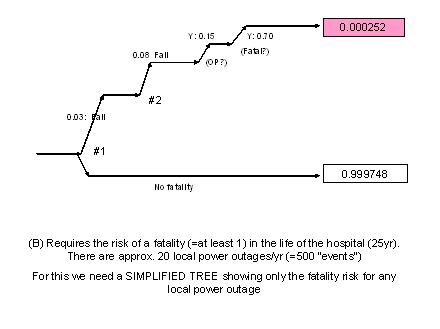
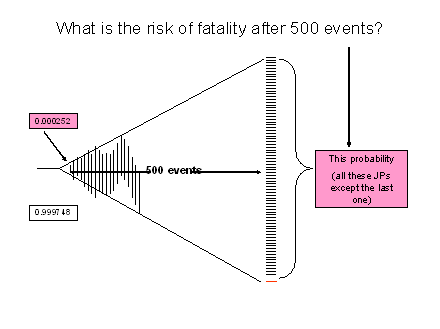
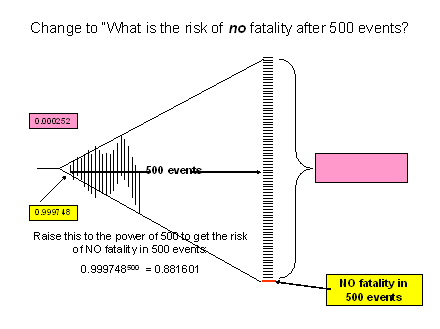
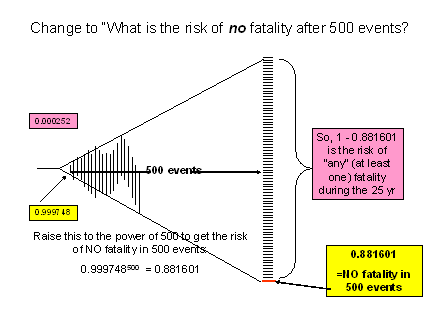
The answer to B is therefore 1- 08816 or 0.11894 (almost 12%)
C asks "by how much would that risk be reduced by the addition
of a THIRD generator with reliability of 98%? This is solved by
inserting another generator in the original tree with a failure
rate of 0.02. The new risk of fatality from a single outage is
5.04E-6 or 0.00000504. The new Pr of NO fatality after a single
event becomes 1- 0.00000504 or 0.99999496 When you raise
THIS to the power of 500, you get 0.997483, and the compliment
(showing the Pr of 'at least one' fatality in that time) is 0.00252.
So the addition of the third generator has reduced the Pr of fatality
in that time from 0.11894 to 0.00252.
D places a $ value on the fatality at $8,000,000. With two generators,
the liability would ($8x106)x(0.11894) = $951,520. With THREE generators,
that liability drops to ($8x106)x(0.00252) = $20,160. So long-range
financial planning might suggest the purchase of a third generator
(even assuming a cost of $60,000-80,000). Of course this is more than
the question asks. The simple answer to D is that the liability with 3
generators drops to about 2% of what it was with 2 generators. This is
seen with probability AND with $$$.