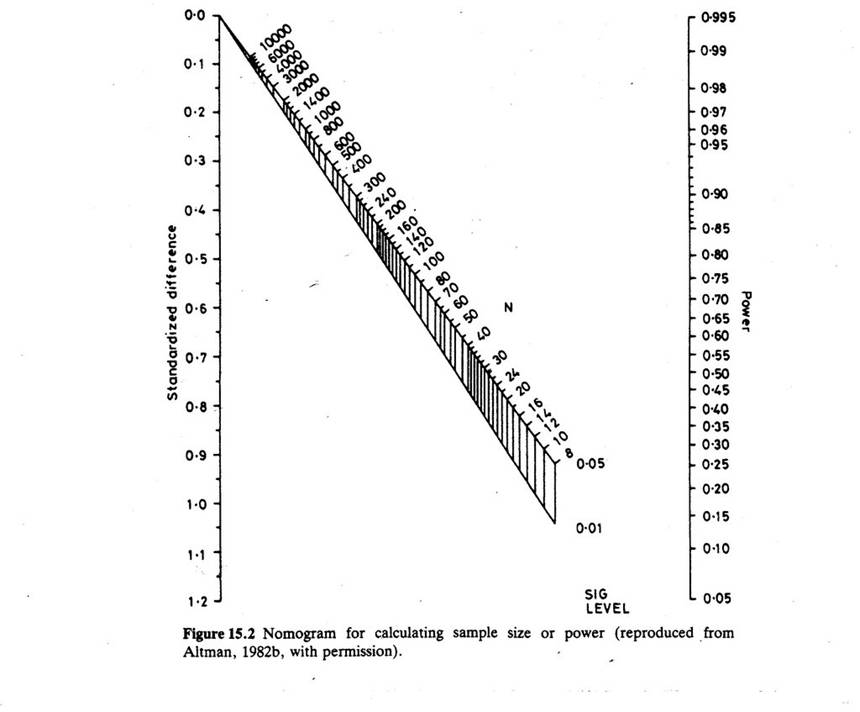
NOMOGRAM FOR POWER ANALYSIS:  notes on how to use....................

Using the nomogram for sample size calculations

(a) continuous data, two independent groups. For example:  Suppose that prior to launching a feeding supplement

program among children in a malnourished area, we are designing a trial among laboratory rats of the supplement

to see if an increase in body mass is achievable. Rats are to be randomly assigned into two groups: a protein-poor

diet (estimated to be equivalent to children's diet in the test region, and a diet with the enhanced protein content.

We know that rats from 2 weeks to 12 weeks should increase by 280 g with a standard deviation of 35 g.  

We anticipate that the supplement will increase weight gain by additional 20 g by week 12.  We want a high probability

of detecting this increase so we set the power to 90% and a 5% significance level.

METHOD:   We need:  Standard deviation of the variable (S)

                                 Clinically relevant difference or effect (δ)

                                 Significance level (α)    

                                 Power: This is the chance of finding the effect if it exists. It is written as:

                                             1 minus the risk of NOT- finding the effect if it did exist (1- β) where

                                             the symbol on the right is a "beta" (in case it does not show on your browser)

     "Standardized difference"  is   Clinically-relevant difference or effect (δ)    =     20    =   0.57  

                                                           Standard deviation (S)                                 35

Use the nomogram with StdDiff at 0.57,   power at 90% (0.90), and rejection level (α) at 0.05  to obtain n = 130 or 65 in each group.

(b) categorical data (binary: two groups)   For example: A new electrical stimulation device for epileptics is being tested.

Patients are able to give themselves a mild, regulated electrical stimulus immediately they feel a seizure might be imminent.

Twenty percent (20%) of these patients could expect to be free of seizures in a 12 month period.  The device would be

considered a success if that rate could be doubled to 40% seizure-free in a year, and we want a 85% probability of finding

this result if it exists (at 99% significance).

METHOD:  Need:  The expected proportion with the outcome in each group (p1 and p2)

                           Significance level (α)

                           Power (α)

                           The Mean between the 'existing' and the 'target' output (p1+p2)/2 is denoted ' '.

(Please note on some browsers this may not appear correctly.  It is described as "p-hat" and resembles a small p with

a circumflex accent on top.)

      "Standardized difference"    is      _ p1 - p2    =    0.4 - 0.2     =  0.2    =    __0.2_  =  0.44

                                                         √(1-)          √0.3(0.7)    √0.21        0.458

       (where is the mean of p1 and p2)

Use the nomogram with StdDiff: 0.44,   power: 85% (0.85), and α as 0.01  to obtain n = 260 or 130 in each group.