PROTEUS

              

 

 

 

 

 

 

 

Solution to number 15

 

•The tree now allows you to easily derive answers to a, b, and c. 
•
•d asks: “the expected life of this reactor is 20 years. What is the probability of a serious incident” occurring in its lifetime?”
(note that we should take this to mean one or more serious incidents [SI] in that time)
To start this process we need a new “tree”

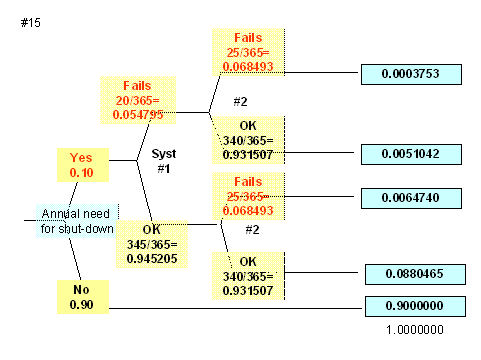
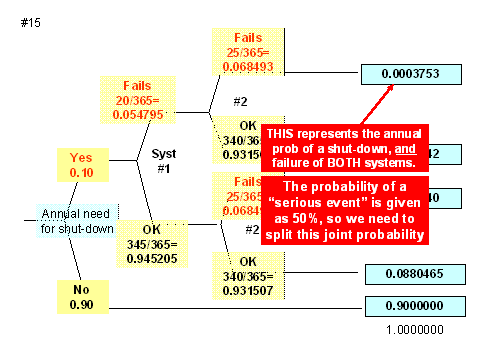
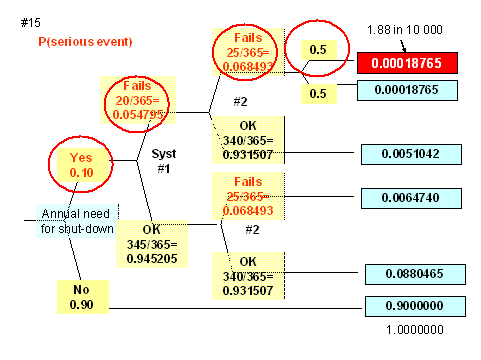
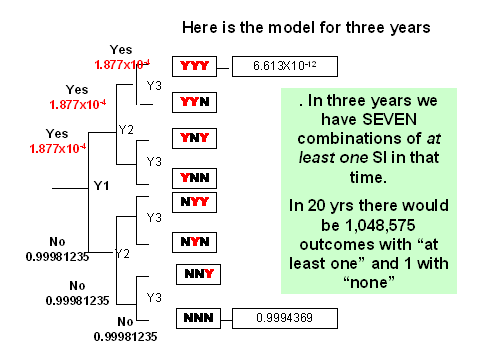
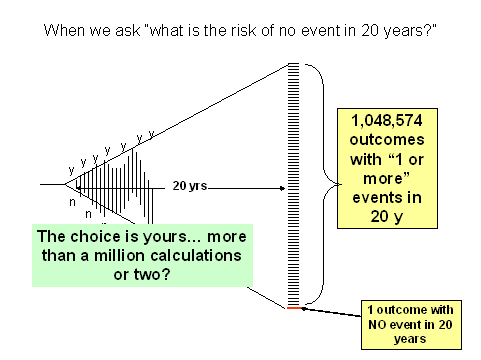
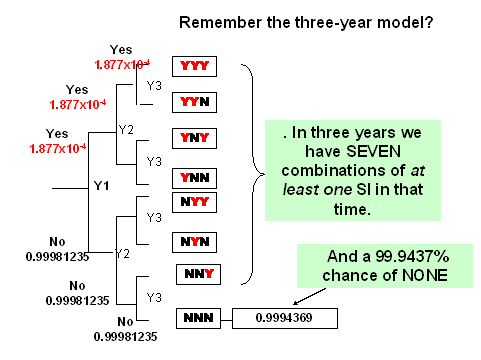
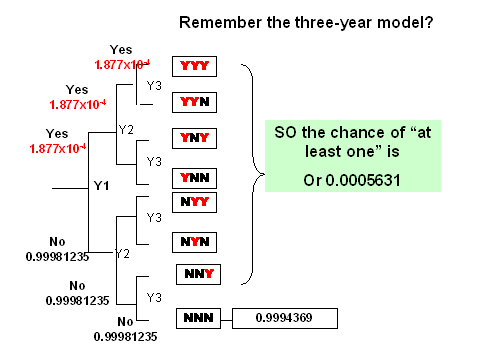
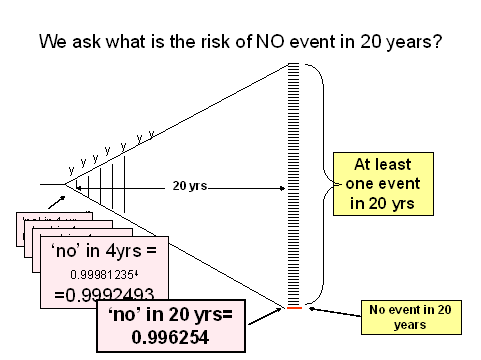
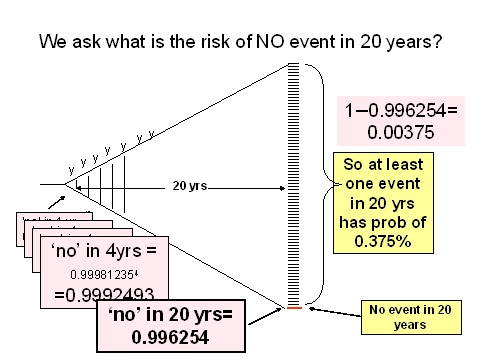
Note that the intuitive answer is NOT correct... you cannot simply multiply the P(event) from one year by 20.  The answer is incorrect.  In this case, because the number of years is small (20) the final answer is still correct to 3 significant figures (0.00375), but for increasing number of exposures or iterations, the error would become more evident.

As an example, suppose the risk of an event per month was 1 in 500 (0.002).  We are interested in the P of one or more of these events happening over a lifetime (70x12 = 840 months).  multiplying 0.002 by 840 yields a "probability" of 1.68 which is impossible. Using the above method, the correct solution would be

  1- {(1-[0.002840]}  or  0.814 or 81.4%

An even more direct confrontation to the intuition is the following:  Suppose the risk of a genetic condition occurs at 0.01 in the population.  What is the probability of having at least one in a group of 100?  The solution is NOT a probability of 1.0, any more than it would be 2.0 in a group of 200 persons!    Instead, for 100, it can be shown to be a little more than 63% and in a group of 200, the probability that at least one occurs in 86.7%